Using the Present Value function PV will allow you to calculate how much to invest today in order to become a millionaire after a certain number of years.
The Format of a PV function is
PV(Rate,Nper, Pmt,FV,Due)
Rate=Interest rate
Nper=The length of period (Usually number of years)
Pmt=Periodic payment
FV=Future Value
Due= 1 if payment due at beginning of a period and Due=0 if payment due at the end of a period.
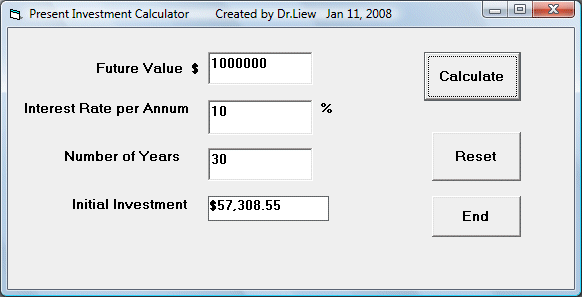
In my example, I am considering one single initial investment in order to earn a certain amount of money in the future, so Pmt is set to 0, and payment due is at the beginning of the period, so it is set at 0, the rest of the values are obtained from the users.
The Format of a PV function is
PV(Rate,Nper, Pmt,FV,Due)
Rate=Interest rate
Nper=The length of period (Usually number of years)
Pmt=Periodic payment
FV=Future Value
Due= 1 if payment due at beginning of a period and Due=0 if payment due at the end of a period.

In my example, I am considering one single initial investment in order to earn a certain amount of money in the future, so Pmt is set to 0, and payment due is at the beginning of the period, so it is set at 0, the rest of the values are obtained from the users.
Code:
Private Sub cmdCal_Click()
Dim F_Money, Int_Rate, Investment As Double
Dim numYear As Single
F_Money = Val(Txt_FV.Text)
Int_Rate = (Val(Txt_Rate.Text) / 100)
numYear = Val(Txt_Year.Text)
Investment = PV(Int_Rate, numYear, 0, F_Money, 1)
Lbl_PV.Caption = Format(-Investment, "$##,###,##0.00")
End Sub
Dim F_Money, Int_Rate, Investment As Double
Dim numYear As Single
F_Money = Val(Txt_FV.Text)
Int_Rate = (Val(Txt_Rate.Text) / 100)
numYear = Val(Txt_Year.Text)
Investment = PV(Int_Rate, numYear, 0, F_Money, 1)
Lbl_PV.Caption = Format(-Investment, "$##,###,##0.00")
End Sub
0 comments:
Post a Comment